Comprendre facilement la Backpropagation
La Backpropagation, est une technique qui peut sembler compliquée à comprendre mais qui est indispensable pour entraîner un réseau de neurones. Si ce mot te paraît encore obscure, alors dans cet article je vais t’aider pas à pas à bien le comprendre.
Dans cette article, tu verras :
- A quoi sert la Backpropagation. ✔
- Les graphes de calcul, qui est le cadre dans lequel on utilise la Backpropagation. ✔
- L’algorithme Backpropation sur les graphes de calcul pour calculer un gradient. ✔
Pourquoi utiliser la Backpropagation ?
La Backpropagation sert à calculer le gradient d’une fonction. Mais sais-tu pourquoi on a besoin de cette technique pour calculer le gradient ? 🤔
Tu devrais déjà savoir que pour entraîner un réseau de neurones, on utilise l’algorithme du gradient. Pour rappel, cette méthode à pour but, à partir d’une fonction ![]() de variable
de variable ![]() à valeurs réelles, de trouver une valeur de
à valeurs réelles, de trouver une valeur de ![]() telle que
telle que ![]() soit la plus petite possible. Elle consiste à construire une suite de paramètres
soit la plus petite possible. Elle consiste à construire une suite de paramètres ![]() ,
, ![]() ,
, ![]() ,
, ![]() telle que :
telle que :
![]()
où ![]() est un nombre appelé le coefficient d’apprentissage (« learning rate » en anglais) et où
est un nombre appelé le coefficient d’apprentissage (« learning rate » en anglais) et où ![]() , est le gradient de
, est le gradient de ![]() en
en ![]() .
.
Ainsi la question est : comment calcule-t-on ce gradient lorsque que ![]() est la fonction de coût d’un réseau de neurones ?
est la fonction de coût d’un réseau de neurones ?
La méthode qu’on apprend aux étudiants à l’école pour évaluer des gradients est la suivante :
- Calculer les fonctions dérivées partielles.
- Évaluer les dérivées partielles.
Cette méthode marche très bien sur des fonctions simples, mais elle devient très mauvaise à appliquer sur des exemples compliqués (surtout dans le cas d’un réseau de neurones), car :
- Calculer les fonctions dérivées partielles est très coûteux si la fonction est compliquée. Et dans un réseau de neurones, la complexité de la fonction est proportionnelle au nombre de couches du réseau.
- Il y a autant de dérivées partielles que de paramètres. Or dans un réseau de neurones, il peut y avoir des millions de paramètres 😬.
La Backpropagation est alors une méthode pour évaluer le gradient de manière beaucoup moins coûteuses 👍.
La différence majeure avec la méthode précédente est que lorsqu’on évalue le gradient, on ne calcule que la valeur de la dérivée partielle au point considéré et non pas la fonction dérivée partielle.
Les graphes de calcul
Pour comprendre la Backpropagation, il est nécessaire de connaître la notion de graphe de calcul (pas d’inquiétude ce n’est pas compliqué 🙂). En effet le graphe de calcul est le cadre général pour utiliser la Backpropagation. On pourra d’ailleurs remarquer qu’un réseau de neurones s’interprète naturellement comme un graphe de calcul.
Qu’est-ce qu’un graphe de calcul ?
Un graphe de calcul est un graphe orienté où les nœuds sont soit des variables soit des opérations, et les arêtes indiquent les membres des opérations. Un tel graphe peut être interprété comme une fonction.
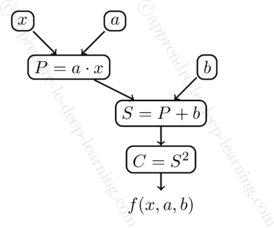
Le plus simple pour comprendre est de considérer un exemple 👍. Prenons la fonction ![]() de trois variables définie par :
de trois variables définie par :
![]()
où les variables ![]() ,
, ![]() et
et ![]() sont des nombres réels. Alors on peut décomposer la fonction
sont des nombres réels. Alors on peut décomposer la fonction ![]() en opérations élémentaires à savoir :
en opérations élémentaires à savoir :
- Un produit
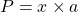 .
. - Une somme
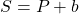 .
. - Un carré
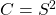 .
.
Ainsi, on peut schématiser la fonction ![]() par le graphe de calcul suivant :
par le graphe de calcul suivant :
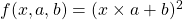 .
.L’algorithme Feedforward
Pour évaluer une fonction à l’aide du graphe de calcul, on utilise l’algorithme Feedforward. Cet algorithme est très intuitif : il consiste à évaluer le résultat de chaque nœud, et de noter le résultat, en parcourant le graphe dans le sens direct.
Par exemple sur la fonction ![]() , si on veut l’évaluer en
, si on veut l’évaluer en ![]() ,
, ![]() et
et ![]() , alors l’algorithme s’applique comme suit :
, alors l’algorithme s’applique comme suit :
- On commence par noter les valeurs des nœuds
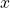 ,
,  et
et 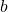 .
. - Ensuite, on calcule la valeur du nœud
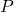 à l’aide des valeurs de
à l’aide des valeurs de 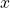 et
et  . Ce qui donne
. Ce qui donne 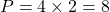 .
. - Puis, on calcule la valeur du nœud
 à l’aide des valeurs de
à l’aide des valeurs de  et
et 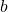 . Ce qui donne
. Ce qui donne 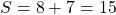 .
. - Enfin, on calcule la valeur du nœud
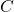 à l’aide de
à l’aide de 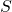 . Ce qui donne
. Ce qui donne 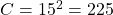 .
.
Sur la figure suivante, note à côté de chaque nœud le résultat de son évaluation.
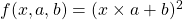 pour évaluer en
pour évaluer en 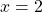 ,
, 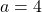 et
et 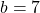 .
.Jusqu’ici rien de bien compliqué 👍.
Comment calculer un gradient par Feedforward
Je vais t’expliquer comment calculer le gradient avec l’algorithme Feedforward. Tu te dis sûrement « quoi ? Je croyais qu’il fallait utiliser la Backpropagation pour calculer le gradient ! » 🤨. Effectivement, dans un réseau de neurones on calcule le gradient par Backpropagation. Mais la Backpropagation n’est pas la seule méthode pour calculer un gradient. On peut aussi le faire là l’aide de Feedforward. Cependant la méthode Feedforward est inutilisable en pratique sur des fonctions avec beaucoup de variables, comme on le verra.
Pourquoi est-ce je présente cette méthode ? Parce que je trouve cette méthode plus intuitive et plus facile à comprendre que la Backpropagation. Et une fois que tu auras compris cette méthode, tu comprendras plus facilement la méthode Backpropagation 👍.
La procédure est la suivante. En parcourant chaque nœud dans le sens directe, on calcule les deux valeurs suivantes :
- Le résultat du nœud.
- Le gradient du résultat du nœud par rapport aux paramètres de la fonction.
Si on prend toujours l’exemple sur la fonction ![]() précédent, pour évaluer son gradient en
précédent, pour évaluer son gradient en ![]() ,
, ![]() et
et ![]() , alors l’algorithme se déroule comme suit :
, alors l’algorithme se déroule comme suit :
- On commence par noter la valeur
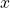 ainsi que son gradient par rapport aux trois variables. Ce qui donne :
ainsi que son gradient par rapport aux trois variables. Ce qui donne :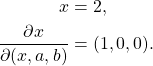
On fait pareil pour les nœuds et
et 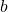 . Ce qui donne :
. Ce qui donne :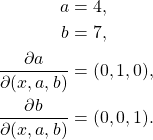
- Ensuite, on calcule pour le nœud
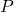 sa valeur et son gradient par rapport au trois variables :
sa valeur et son gradient par rapport au trois variables :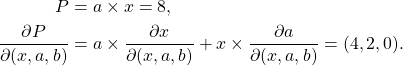
- Puis, on passe au nœud
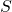 :
: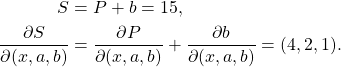
- Enfin, pour le nœud
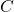 :
: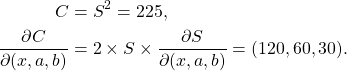
Ce qui permet d’en déduire le gradient :
![]()
Le schémas suivant résume les calculs.
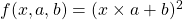 pour calculer le gradient en
pour calculer le gradient en 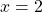 ,
, 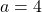 et
et 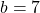 .
.Voilà, comment calculer un gradient par Feedforward👍.
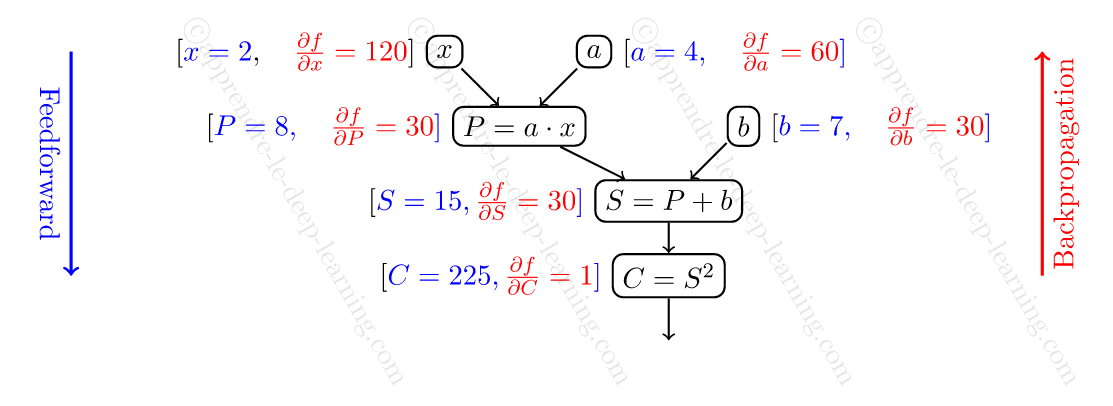
Comment calculer le gradient avec la Backpropagation
Tu viens de voir comment calculer un gradient par Feedforward. Mais cette méthode n’est pas optimale et est plus coûteuse que la Backpropagation. En effet dans la méthode Feedforward, pour chaque nœud on doit calculer un gradient, qui est un vecteur de taille égale au nombre de paramètres. Alors que dans Backpropagation, il suffit seulement de calculer la dérivée partielle par rapport à une seule valeur, ce qui donne un nombre et non pas un vecteur !
L’algorithme Backpropagation se déroule de la manière suivante :
- On applique l’algorithme Feedforward pour calculer la valeur de tous les nœuds (seulement la valeur, et non pas le gradient).
- Ensuite on parcourt les nœuds dans le sens inverse, pour calculer la dérivée partielle de
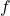 par rapport au nœud.
par rapport au nœud.
Illustrons cette algorithme toujours sur l’exemple ![]() précédent.
précédent.
- On applique l’algorithme Feedforward. Ce qui donne
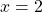 ,
, 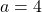 ,
, 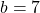 ,
, 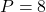 ,
, 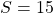 ,
, 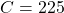 .
. - Ensuite on parcourt les nœuds à partir de la fin pour calculer la dérivée partielle de
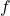 par rapport au nœud. Ce qui donne en commençant par
par rapport au nœud. Ce qui donne en commençant par 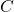 , puique
, puique 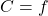 :
:![Rendered by QuickLaTeX.com \[\frac{\partial f}{\partial C} = 1.\]](https://apprendre-le-deep-learning.com/wp-content/ql-cache/quicklatex.com-2336fdb971ae266bae50069bac060f79_l3.png)
- Ensuite, passe au nœud
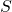 :
:![Rendered by QuickLaTeX.com \[\frac{\partial f}{\partial S} = \frac{\partial f}{\partial C} \times \frac{\partial C}{\partial S} = \frac{\partial f}{\partial C} \times 2 S = 30.\]](https://apprendre-le-deep-learning.com/wp-content/ql-cache/quicklatex.com-714c65395348699e1c973f732d005b95_l3.png)
- Ensuite on passe aux nœuds
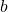 et
et 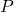 :
: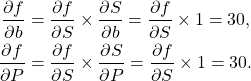
- Enfin on passe aux nœuds
 et
et  :
: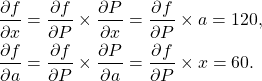
Ainsi on retrouve bien mêmes valeurs qu’avec la méthode Feedforward 😋.
A noter que pour calculer les valeurs des dérivées partielles de chaque nœud, on a besoin des valeurs des nœuds parents, d’où la nécessité de faire Feedforward.
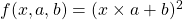 pour calculer le gradient en
pour calculer le gradient en 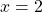 ,
, 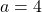 et
et 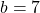 .
.Pour finir, le calcul est illustré par le schémas suivant.
Voilà maintenant tu es capable de calculer un gradient à l’aide de la Backpropagation😀.
Mot de la fin
Si cette article t’a aidé ou bien si tu as des questions n’hésite pas à le dire en commentaire 👌.
Concernant son utilisation sur les réseaux de neurones, il y a une chose à savoir. Dans cette présentation, j’ai traité le cas où les résultats des nœuds sont des nombres. Or on peut généraliser au cas où les résultats des nœuds sont des vecteurs (ou même des tenseurs). Tout se passe de la même manière, à part que les valeurs et les dérivées partielles ne sont plus des nombres mais des vecteurs. C’est le cas de l’implémentation par Tensorflow et PyTorch: chaque nœud est une couche du réseau (c-à-d une liste de neurones) et les opérations entre les nœuds sont des opérations matricielles.
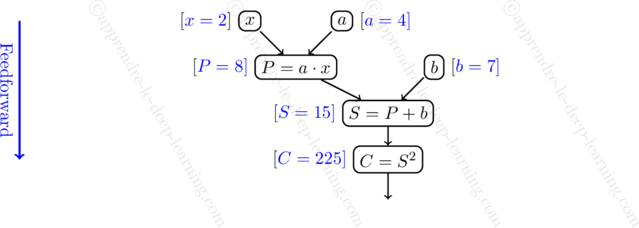
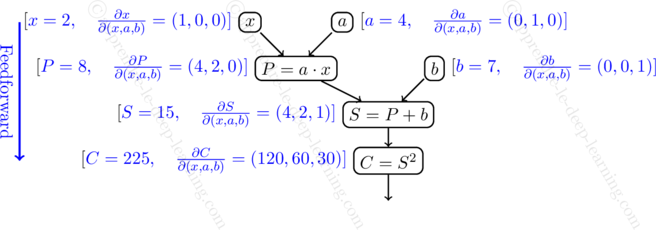
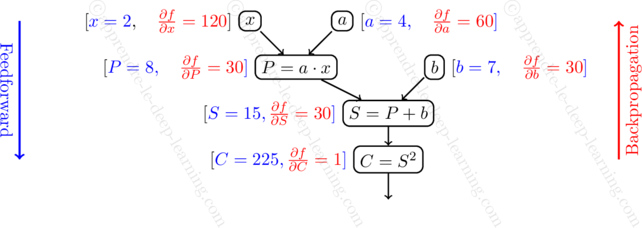




4 commentaires
Pascal · 27 février 2023 à 19h21
Merci pour ces explications très pédagogiques ! Je suis arrivé sur votre site en faisant une recherche sur l’intérêt de la back propagation par rapport à la forward propagation. C’est clair maintenant.
Je pense qu’il y a une petite erreur dans le dessin sur la forward-propagation où le résultat final (60, 30, 15) n’est pas celui indiqué dans le texte (120, 60, 30).
Auguste Hoang · 13 mars 2023 à 0h29
Bonjour Pascal,
Il y a effectivement une erreur sur le dessin.
Je l’ai corrigé.
Merci beaucoup pour ton commentaire !
Bruno · 24 novembre 2024 à 17h34
Super clair. L’approfondissement avec des vecteurs au lieu des nœuds serait grandement apprécié. Surtout que l’on trouve très difficilement cette explication avec un exemple numérique.
Hadefi · 15 février 2025 à 5h02
The clarity and simplicity of the article shows that the author has a good command of the subject.
Thank you Hoang.