Tout savoir sur U-Net : l’architecture révolutionnaire pour la segmentation d’images

Publié par Auguste Hoang le 13 mai 202313 mai 2023

Partagez sur les réseaux sociaux !

Lorsque les médecins regardent des images médicales, comme des IRM ou des scans, ils doivent être capables de distinguer les différentes parties du corps ou les différents tissus. Cela s’appelle la segmentation d’images.

De manière générale, la segmentation d’image est un problème qui prend en entrée une image et qui en sortie cherche à prédire la classe de chaque pixel. Autrement dit, l’entrée est un tableau avec des dimensions pour la largeur, la hauteur et les couleurs de l’image, et la sortie est un tableau avec les mêmes dimensions que l’image originale, mais chaque pixel est désormais étiqueté avec une classe.

Un exemple de ce genre de problème est donnée dans la compétition Kaggle 2018 Data Science Bowl. Dans cette compétition, à partir d’une image médicale, il faut classifier les zones qui représentent les cellules comme illustré dans la figure suivante.

Fig. : Exemple de segmentation. A gauche se trouvent des images médicales et à droite est associé un masque (avec des pixels blancs ou noirs) indiquant les cellules.

Afin de résoudre ce type de problème, il existe une architecture de réseau de neurones particulièrement efficace introduite dans cet article. Cette architecture s’appelle U-Net en raison de sa forme en U.

On explique dans la suite de cet article les détails de cette architecture.

Les 3 ingrédients de U-Net

L’architecture est composée essentiellement de 3 ingrédients qui ont chacun un rôle bien précis: les blocs Downsample, Upsample et Connexion Résiduelle.

Bloc Downsample

Le premier bloc de calcul est le bloc Downsample (pour sous-échantillonnage). Le but de ce bloc est réduire par 2 la taille de l’image en entrée et d’augmenter par 2 le nombre de channels. Autrement dit, si le tenseur en entré est de foramt $[w,h,c]$ , alors la sortie sera de format $[\frac{w}{2}, \frac{h}{2}, 2c]$ .

Ce bloc est constitué de :

Une unité de calcul MaxPool de stride $2 \times 2$ . Cela a pour effet de diviser la taille de l’image par 2.
Une unité de calcul Convolution 2D dont le kernel est de taille $3 \times 3$ avec activation Relu et le nombre de channels vaut $2c$ , où $c$ est le nombre de channels du tenseur d’entrée.
Une deuxième unité Convolution 2D de taille $3 \times 3$ avec activation Relu et le nombre de channels vaut $2c$ .

En résumé cette opération diminue le nombre de pixels et augmente le nombre d’informations de chaque pixel. Il faut imaginer que l’on regroupe des blocs de 2×2 pixels, et chaque pixel résultant contiendra l’information de ces 4 pixels d’origine. Cette opération est souvent utilisée dans les réseaux de neurones de convolution pour la classification d’images.

Bloc Upsample

Le deuxième bloc de calcul est le bloc Upsample (pour sur-échantillonnage). Il a pour rôle exactement l’inverse du bloc Upsample. Il multiplie par 2 la taille de l’image en entrée et réduit par 2 le nombre de channels. Autrement dit, si le tenseur en entrée est de format $[w,h,c]$ , alors la sortie sera de format $[2w, 2h, \tfrac{c}{2}]$ .

Ce bloc est constitué de :

Une unité de calcul UpSample de stride $2 \times 2$ . Cela a pour effet d’augmenter la taille de l’image par 2.
Une unité de calcul Convolution 2D dont le noyau est de taille $2 \times 2$ avec activation Relu et et le nombre de channels vaut $\tfrac{c}{2}$ , où $c$ est le nombre de channels du tenseur d’entrée.

De manière analogue que dans le cas Downsample, cette opération augmente le nombre de pixels et il diminue le nombre d’informations de chaque pixel.

Bloc Connexion Résiduelle

Dans les réseaux de neurones, il est important de pouvoir conserver les informations importantes tout au long du processus d’apprentissage. Pour cela, on utilise une technique appelée connexion résiduelle (ou skip connection en anglais). Cette technique consiste à prendre le résultat d’une unité de calcul et à le combiner avec le résultat d’une unité de calcul précédente avant de le donner en entrée à l’unité de calcul suivante. Cela permet de conserver les informations importantes et d’éviter la disparition de gradient, ce qui améliore la performance du modèle.

Ce bloc est constitué de :

Une concaténation de de deux tenseurs de même format $[w,h,c]$ . Le résultat est donc un tenseur de format $[w,h,2c]$ .
Une unité de calcul Convolution 2D dont le noyau est de taille $3 \times 3$ avec activation Relu et le nombre de channels vaut $c$ .
Une deuxième unité Convolution 2D de taille $3 \times 3$ avec activation Relu et le nombre de channels vaut $c$ .

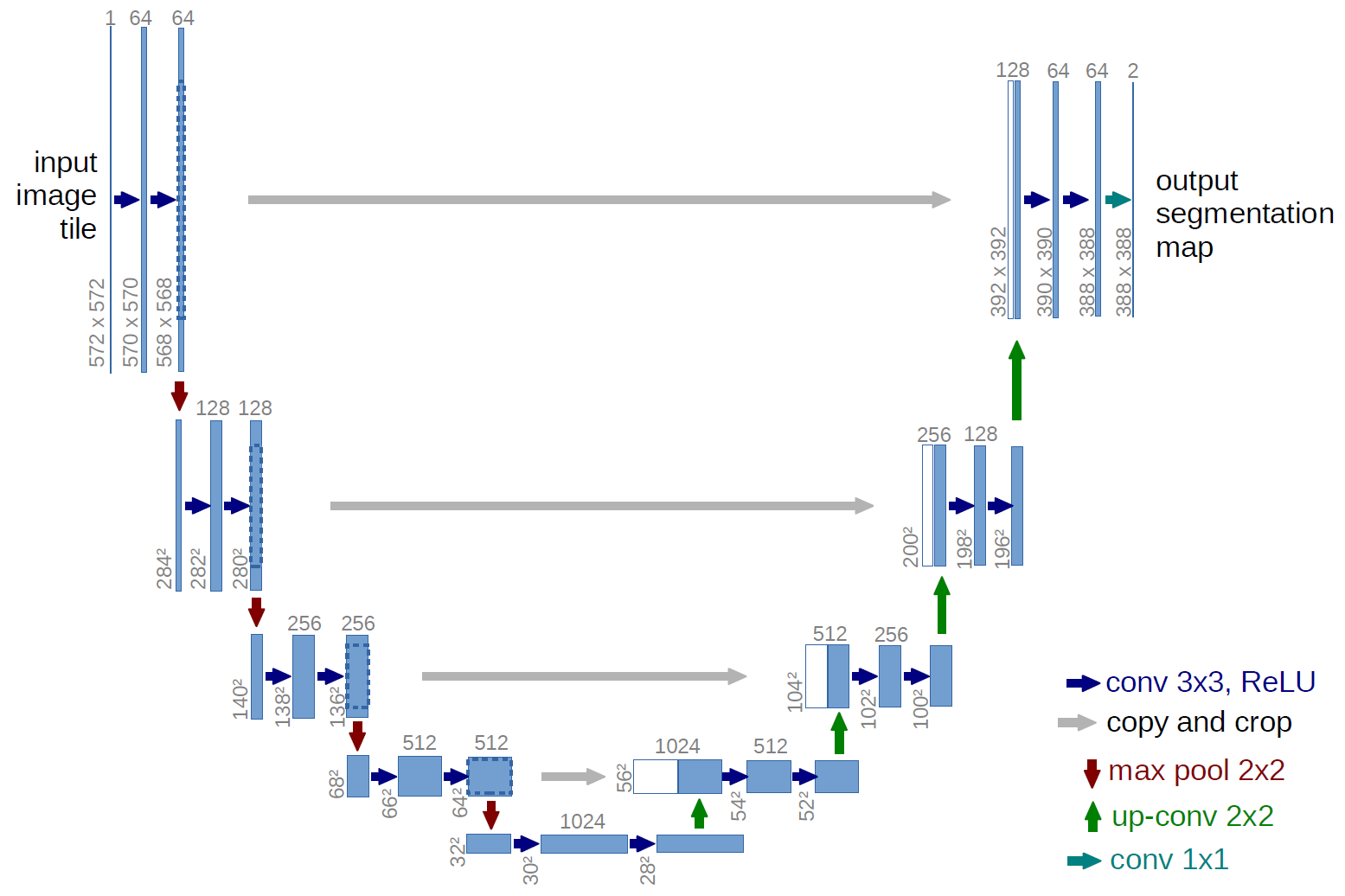
Architecture de U-Net

Nous pouvons maintenant décrire l’architecture de U-net.

D’abord, l’image en entrée va passer dans une double convolution pour ajuster la taille de la dimension channel.
Deuxièmement, il y a une succession $N$ de blocs Downsample, où $N$ est un entier indiquant la profondeur du réseau (à titre d’exemple on choisira $N=3$ ). Cette partie constitue la branche gauche du U.
Troisièmement, il y a une succession de $N$ blocs Upsample combinés avec des connexions résiduelles avec les blocs Downsample. Cette partie constitue la branche droite du U.
Enfin, on applique une convolution à la dernière couche pour ajuster la taille de la dimension channel.

Les détails sont présentés sur le schémas suivant, où $d$ désigne les dimensions de l’image en entrée (hauteur et largeur) et $c$ le nombre de channels de la première convolution.

Rendered by QuickLaTeX.com — Fig. 1 : Schémas représentatif de l’architecture U-Net.

Une chose importante à noter est que cette architecture n’est valable que si les dimensions de l’image d’entrée est suffisamment divisible par 2 (par exemple ici, il faut que $d$ soit divisible par 8) et qu’on utilise des convolutions avec le padding égale à « same ». Dans le cas contraire, les entrées des blocs Connexion Résiduel ne sont plus de même dimension, et il faut alors rogner les images, comme le fait l’article originel.

Implémentation de U-net avec Keras

Voici un exemple d’implémentation de U-Net avec la librairie keras. Dans cet exemple on prend le cas le plus simple où la taille de l’image est suffisamment divisible par 2.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

import keras
import tensorflow

def UNet():
def DoubleConvolution(filters, inputs):
"""
filters : outputs filter dimension
inputs : input tensor
"""
y = keras.layers.Conv2D(filters = filters, kernel_size = (3,3), padding = 'same', activation='relu')(inputs)
y = keras.layers.Conv2D(filters = filters, kernel_size = (3,3), padding = 'same', activation='relu')(y)
return y

def DownSample(filters, inputs):
"""
filters : outputs filter dimension
inputs : input tensor
"""
y = keras.layers.MaxPooling2D(pool_size = (2, 2), padding='valid')(inputs)
y = DoubleConvolution(filters, y)
return y

def UpSample(filters, inputs):
"""
filters : outputs filter dimension
inputs : input tensor
"""
y = keras.layers.UpSampling2D(size=(2, 2))(inputs)
y = keras.layers.Conv2D(filters = filters, kernel_size = (3,3), padding = 'same', activation='relu')(y)
return Out

def ResidualConnection(filters, input_1, input_2):
"""
filters : outputs filter dimension
input_1 : first input
input_2 : second input
"""
y = keras.layers.Concatenate(axis=-1)([input_1, input_2])
y = DoubleConvolution(filters, y)
return y

Input = keras.layers.Input( shape=(800,800,3) ) # shape = (800,800,3)

# Contraction/Downsampling path
Conv0 = DoubleConvolution(64, Input) # shape = (800,800,64)
Conv1 = DownSample(128, Conv0) # shape = (400,400,128)
Conv2 = DownSample(256, Conv0) # shape = (200,200,256)
Conv3 = DownSample(512, Conv0) # shape = (100,100,512)

# Expensive/Upsampling path
UpConv2 = UpSample(256, Conv3) # shape = (200,200,256)
Res2 = ResidualConnection(256, Conv2, UpConv2) # shape = (200,200,256)

UpConv1 = UpSample(128, Res2) # shape = (400,400,128)
Res1 = ResidualConnection(128, Conv1, UpConv1) # shape = (400,400,128)

UpConv0 = UpSample(64, Res1) # shape = (800,800,64)
Res0 = ResidualConnection(64, Conv0, UpConv0) # shape = (800,800,64)

Output = keras.layers.Dense(units = 2, activation='softmax')(UpConv1) # shape = (800,800,2)

return keras.models.Model( Input, Output )

Voilà, maintenant tu sais tout sur l’architecture de Unet ! 👍

N’hésites à pas à partager cet article s’il t’a plu. Et si tu as des questions tu peux les poser en commentaire.

Catégories : CodeDeep LearningPython

Tout savoir sur U-Net : l’architecture révolutionnaire pour la segmentation d’images