Comprendre comment marche la méthode du gradient
La méthode du gradient est un outil indispensable en machine learning. Dans la plupart des algorithmes, on doit souvent trouver les paramètres qui minimisent une fonction.
Si par exemple la fonction à minimiser est ![]() , alors on sait que le minimum (ou maximum si
, alors on sait que le minimum (ou maximum si ![]() ), est obtenue pour
), est obtenue pour ![]() . Malheureusement pour les autres fonctions, il n’y a pas toujours de formules magiques pour obtenir ce minimum, surtout lorsque la fonction admet plusieurs variables.
. Malheureusement pour les autres fonctions, il n’y a pas toujours de formules magiques pour obtenir ce minimum, surtout lorsque la fonction admet plusieurs variables.
Cependant, il existe une méthode relativement efficace qui permet de résoudre ce problème pour n’importe quelle fonctions. C’est la méthode du gradient. Et c’est elle qui est utilisée pour entraîner un réseau de neurones lorsque l’on fait de la backpropagation.
Dans cet article, tu vas comprendre:
- Comment fonctionne cette méthode ✔
- Pourquoi elle fonctionne ✔
- Ses limites d’utilisation ✔
D’où vient la méthode du gradient ?
Le cadre général d’utilisation de la méthode de gradient est le suivant. On dispose d’une fonction ![]() de plusieurs variables
de plusieurs variables ![]() dont on sait évaluer sa valeur et son gradient en tout point
dont on sait évaluer sa valeur et son gradient en tout point ![]() . La question est de trouver le point
. La question est de trouver le point ![]() qui minimise
qui minimise ![]() .
.
Le principe général de la méthode de gradient est de partir d’un point ![]() au hasard, et de le déplacer d’un petit pas pour faire diminuer la valeur
au hasard, et de le déplacer d’un petit pas pour faire diminuer la valeur ![]() .
.
Pour comprendre comment faire déplacer ![]() , il faut utiliser le résultat mathématique suivant. Si
, il faut utiliser le résultat mathématique suivant. Si ![]() est fonction de une seule variable
est fonction de une seule variable ![]() , alors on peut faire l’approximation suivante:
, alors on peut faire l’approximation suivante:
![]()
lorsque ![]() est un nombre suffisamment petit (on rappelle que
est un nombre suffisamment petit (on rappelle que ![]() est la dérivée de
est la dérivée de ![]() en
en ![]() ). Cette formule s’appelle le développement limité de
). Cette formule s’appelle le développement limité de ![]() .
.
Ce qu’il faut comprendre de cette formule est que si on change ![]() d’une petite valeur
d’une petite valeur ![]() , alors on change
, alors on change ![]() d’une valeur proportionnelle à
d’une valeur proportionnelle à ![]() , à savoir
, à savoir ![]() 👍.
👍.
En particulier si on veut faire diminuer ![]() , alors il faut prendre
, alors il faut prendre ![]() un nombre de signe opposé à
un nombre de signe opposé à ![]() 👍.
👍.
Pour les fonctions de plusieurs variables
Qu’en est-il des fonctions à plusieurs variables ? Nous avons expliqué la formule du développement limité pour des fonctions à une seule variable. On peut facilement la généraliser pour les fonctions de plusieurs variables.
Si ![]() est une fonction de plusieurs variables
est une fonction de plusieurs variables ![]() , alors en figeant toutes les variables sauf une, on se ramène à une fonction d’une seule variable. Donc si on fige toutes les composantes sauf
, alors en figeant toutes les variables sauf une, on se ramène à une fonction d’une seule variable. Donc si on fige toutes les composantes sauf ![]() , on obtient la formule:
, on obtient la formule:
![]()
où ![]() est un petit nombre et
est un petit nombre et ![]() est la dérivée partielle de
est la dérivée partielle de ![]() par rapport à
par rapport à ![]() .
.
En itérant ce procédé sur toutes les composantes, on peut en déduire que si ![]() sont des nombres assez petits, alors:
sont des nombres assez petits, alors:
![]()
La dernière somme peut s’écrire comme étant ![]() le produit scalaire entre le gradient de
le produit scalaire entre le gradient de ![]() en
en ![]() et le vecteur
et le vecteur ![]() . Autrement dit la formule précédente peut s’écrire de manière plus compacte:
. Autrement dit la formule précédente peut s’écrire de manière plus compacte:
![]()
En conséquence, si ![]() est un petit vecteur dans la direction opposée au gradient
est un petit vecteur dans la direction opposée au gradient ![]() , alors le produit scalaire
, alors le produit scalaire ![]() est négatif et donc
est négatif et donc ![]() est strictement inférieur à
est strictement inférieur à ![]() .
.
Voilà le principe fondamental de la méhode du gradient 👌.
Algorithme de la méthode du gradient
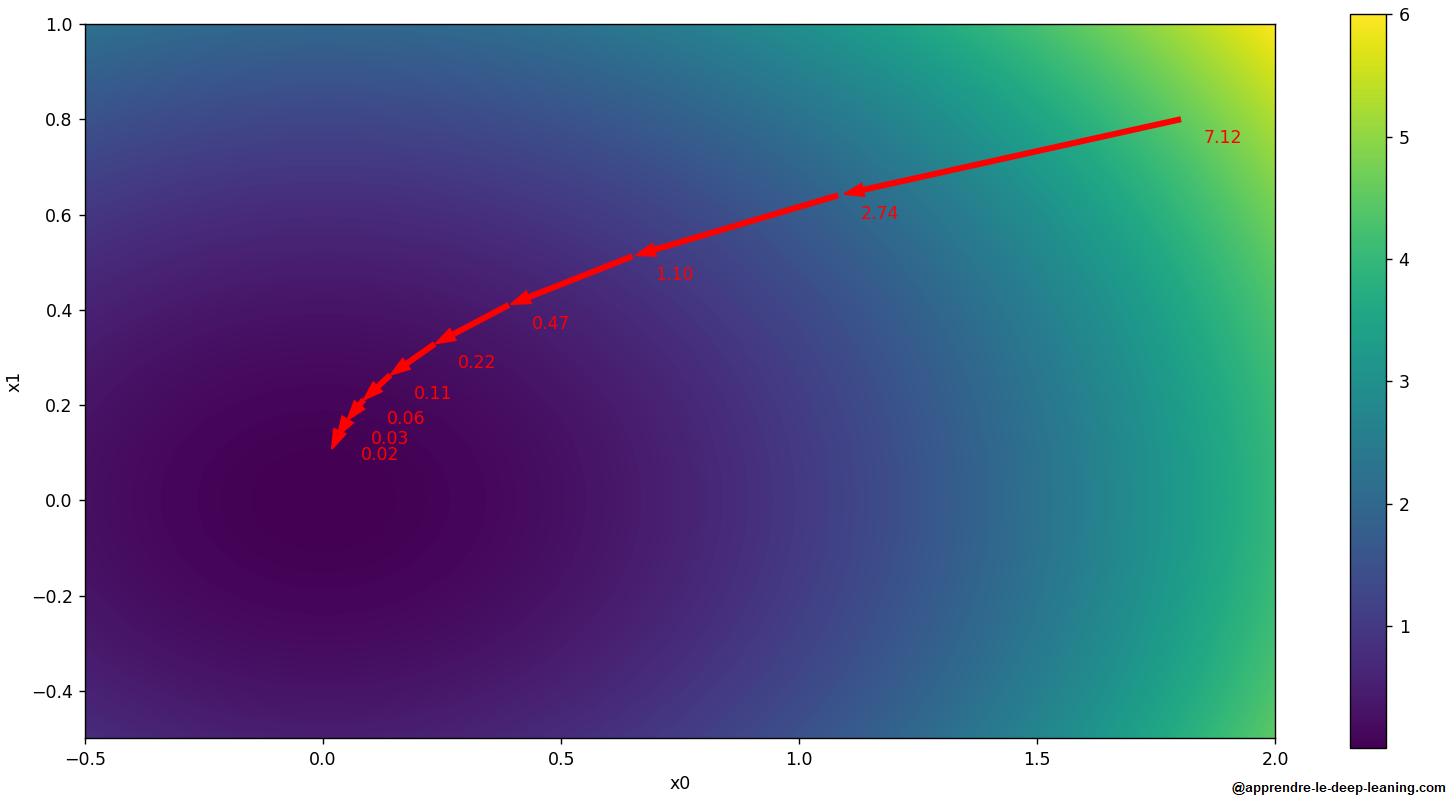
Nous avons vu que si on déplace ![]() d’un petit pas dans la direction opposé au gradient, alors on fait diminuer
d’un petit pas dans la direction opposé au gradient, alors on fait diminuer ![]() . La méthode du gradient consiste à répéter cette opération.
. La méthode du gradient consiste à répéter cette opération.
L’algorithme se présente de la manière suivante :
- Choisir une petite valeur
 , appelée learning rate (ou coefficient d’apprentissage).
, appelée learning rate (ou coefficient d’apprentissage). - Initialiser aléatoirement un point
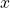 .
. - Répéter un nombre fini de fois:
- Calculer
 , le gradient de
, le gradient de 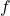 en
en 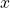 .
. - Changer
 .
.
- Calculer
- Renvoyer la valeur de
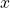 .
.
Le point ![]() renvoyé est alors une estimation du paramètre qui minimise
renvoyé est alors une estimation du paramètre qui minimise ![]() .
.
Il y a plusieurs façons de choisir le nombre d’itérations de l’étape 3:
- Soit on le répète un nombre de fois prédéterminé (par exemple 100).
- Soit on s’arrête lorsque
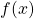 ne diminue plus ou diminue très peu.
ne diminue plus ou diminue très peu.
Le problème du choix du learning rate
Lorsqu’on veut appliquer la méthode du gradient, il faut choisir le learning rate ![]() . Si on choisit un learning rate trop petit, alors il faudra plus d’étapes pour converger le minimum, et si on choisit un learning rate trop grand, alors on va louper le minimum 🤔.
. Si on choisit un learning rate trop petit, alors il faudra plus d’étapes pour converger le minimum, et si on choisit un learning rate trop grand, alors on va louper le minimum 🤔.
Pour comprendre ce phénomène, nous allons l’illustrer par exemple simple. Admettons que l’on veuille minimiser la fonction d’une seule variable ![]() . Si on applique l’algorithme avec un learning rate
. Si on applique l’algorithme avec un learning rate ![]() , et que l’on note
, et que l’on note ![]() la valeur de
la valeur de ![]() à l’étape initial et
à l’étape initial et ![]() la valeur de
la valeur de ![]() à l’étape
à l’étape ![]() . Alors on a la formule:
. Alors on a la formule:
![]()
Comme la dérivé de ![]() vaut
vaut ![]() , on peut réécrire la formule précédente en:
, on peut réécrire la formule précédente en:
![]()
Ainsi la suite ![]() est une suite géométrique de raison
est une suite géométrique de raison ![]() , autrement dit pour tout
, autrement dit pour tout ![]() , on a:
, on a:
![]()
Il y a alors 3 possibilités:
- Soit
 , auquel cas la raison est entre
, auquel cas la raison est entre  et
et  , et la suite
, et la suite  tends vers le minimum
tends vers le minimum  .
. - Soit
 , auquel cas la raison est entre
, auquel cas la raison est entre  et
et  , et la suite
, et la suite  tends vers le minimum
tends vers le minimum  , mais en oscillant.
, mais en oscillant. - Soit
 , auquel cas la raison est
, auquel cas la raison est  , et la suite
, et la suite  diverge.
diverge.
Dans cet exemple il faut que ![]() soit entre
soit entre ![]() et
et ![]() pour que l’algorithme converge vers le bon résultat. A noter que si
pour que l’algorithme converge vers le bon résultat. A noter que si ![]() est trop proche de
est trop proche de ![]() , alors la raison vaudra environ
, alors la raison vaudra environ ![]() , et donc l’algorithme ne convergera pratiquement pas 😬.
, et donc l’algorithme ne convergera pratiquement pas 😬.
Pour une fonction ![]() quelconque, il faut choisir
quelconque, il faut choisir ![]() entre
entre ![]() et
et ![]() , où
, où ![]() est la dérivée seconde de
est la dérivée seconde de ![]() au point minimum pour que l’algorithme converge, et idéalement prendre
au point minimum pour que l’algorithme converge, et idéalement prendre ![]() autour de
autour de ![]() pour que l’algorithme ne converge pas trop lentement. Le problème est qu’on ne peut pas calculer
pour que l’algorithme ne converge pas trop lentement. Le problème est qu’on ne peut pas calculer ![]() vu que l’on ne connaît pas le point minimum…😕
vu que l’on ne connaît pas le point minimum…😕
A cause de ce problème du choix de learning rate, il y a des variantes qui permettent d’ajuster le learning rate au cours de l’algorithme 😀. Citons les principaux:
- RProp (Resilient backPropagation).
- RMSProp (Root Mean Square Propagation).
- AdaGrad (Adaptative Gradient).
- Adam (Adaptative moment Estimation).
Les limites de la méthode du gradient
Bien qu’elle s’applique à pratiquement n’importe quelle situation (la seule condition est que l’on puisse calculer le gradient de ![]() ), la méthode du gradient admet des inconvénients:
), la méthode du gradient admet des inconvénients:
- L’algorithme peut retourner un minimum local de
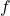 qui n’est pas un minimum global.
qui n’est pas un minimum global. - On a vu qu’il faut choisir un bon learning pour que l’algorithme converge. Mais il y a des cas où il n’y aucun bon learning rate ! En effet, si on considère la fonction de deux variables
![Rendered by QuickLaTeX.com \[f(x,y) = x^2 + 100y^2,\]](https://apprendre-le-deep-learning.com/wp-content/ql-cache/quicklatex.com-21c8d2c7af83ed71ea0d49c06cb43d2a_l3.png)
alors la dérivée seconde de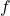 est une matrice qui a deux valeurs propres
est une matrice qui a deux valeurs propres  et
et  . Il faut donc que learning rate soit inférieur à
. Il faut donc que learning rate soit inférieur à  pour que l’algorithme converge, et il faut qu’il soit de l’ordre de
pour que l’algorithme converge, et il faut qu’il soit de l’ordre de  pour que l’algorithme ne converge pas trop lentement. Or il n’y a aucune valeur de
pour que l’algorithme ne converge pas trop lentement. Or il n’y a aucune valeur de 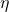 qui vérifie ces deux conditions 😕.
qui vérifie ces deux conditions 😕.
Conclusion
Maintenant tu connais toutes les explications de méthode du gradient 🙂.
Si tu as des remarques ou des questions, alors n’hésite pas à le dire en commentaire.



0 commentaire