Coder simplement un réseau de neurones from scratch
Dans cet article tu vas apprendre à coder un réseau de neurones from scratch.
Les réseaux de neurones sont des modèles très sophistiqués de Machine-Learning. En effet, on peut avoir de nombreuses structures telles que : les Multi-Layer Perceptrons (MLP), les Réseaux de convolutions (CNN), les réseaux récurrents (RNN), etc…
Afin de rendre ce tutoriel simple, je vais te montrer comment implémenter en quelques lignes un Multi-Layer Perceptrons avec fonction d’activation sigmoïde. 👌
Dans cet article tu vas appendre pas à pas :
- Implémenter un Multi-Layer Perceptrons. ✔
- Implémenter l’entraînement par la Backpropagation. ✔
- Tester sur des données réelles. ✔
Pourquoi coder un réseau de neurones from scratch ?
Tu dois sûrement te demander « pourquoi coder un réseau de neurones alors qu’il en existe déjà des librairie qui le font comme Tensorflow et PyTorch ? » 🤔.
La réponse est parce que toutes les librairies de réseaux de neurones sont des boîtes noires 🤨. C’est-à-dire qu’on ne sait pas comment elles fonctionnent, mais on sait juste qu’elles fonctionnent (la plupart du temps…).
Par exemple à l’école ton professeur a dû t’apprendre à faire des multiplications à la main avant de t’apprendre à utiliser la calculatrice, n’est-ce pas ? C’est pour que tu comprennes comment fonctionne la multiplication et comment la calculatrice fait pour faire des multiplications.
Il se trouve que c’est pareil pour les réseaux de neurones. Si tu veux apprendre à utiliser un réseaux de neurones, il faudra comprendre comment fonctionne la boîte noire. 👍
Le Multi-Layer Perceptron (MLP)
Le MLP est l’architecture de réseau de neurones le plus simple à coder. Elle est constituée de couches (=Layer) successives de neurones, où chaque couches est entièrement connectée à la couche précédente.
Si tu n’as pas lu cet article qui explique la Backpropagation, alors je te conseille fortement de le faire pour comprendre la suite 👍. On y explique comment construire un graphe de calcul afin de faire de faire de la Backpropagation.
Dans le cas d’un MLP, le réseau de neurones sera représenté par un graphe. On pourrait représenter chaque nœud du graphe par un seul neurone (i.e. Perceptron), mais il est plus simple de représenter un nœud par une couche (=Layer). Ainsi le résultat d’un nœud n’est plus un nombre mais un vecteur et le graphe devient linéaire, ce qui le rend plus simple à implémenter.
Les prérequis
La manière dont nous allons coder le réseau de neurones va être très proche de celle utilisée par TensorFlow et PyTorch, c’est à dire que nous allons utiliser la notion de couche de calcul, ou Layer en anglais.
Un layer correspond à un nœud dans le graphe de calcul, autrement dit à une opération. Ici on aura besoin de deux types d’opérations.
- Les transformations linéaires (ou plutôt affine). Cette opération prend en entrée un vecteur
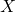 et renvoie en sortie le vecteur :
et renvoie en sortie le vecteur :![Rendered by QuickLaTeX.com \[Y = W \cdot X + B,\]](https://apprendre-le-deep-learning.com/wp-content/ql-cache/quicklatex.com-822d9c37a0644c68e629b725ba7de883_l3.png)
où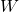 et
et 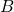 sont les paramètres de l’opération appelé weight (le poids) et bias (le biais). Si
sont les paramètres de l’opération appelé weight (le poids) et bias (le biais). Si 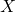 est de taille
est de taille 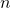 et
et 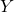 de taille
de taille 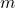 alors
alors 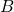 est un vecteur de taille
est un vecteur de taille 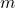 et
et 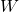 une matrice de format
une matrice de format 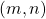 .
. - L’activation sigmoïde. Cette opération prend en entrée un vecteur
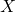 et renvoie en sortie le vecteur :
et renvoie en sortie le vecteur :![Rendered by QuickLaTeX.com \[Y = 1 / (1+\exp(-X)),\]](https://apprendre-le-deep-learning.com/wp-content/ql-cache/quicklatex.com-9deb392fe1e2166a27b1859aae804e68_l3.png)
où toute les opérations se font composantes par composantes, c’est-à-dire que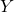 est une vecteur de même taille que
est une vecteur de même taille que 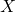 et que
et que 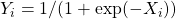 pour toutes les composantes
pour toutes les composantes 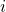 .
.
Nous allons faire de la Programmation Orienté Objet, c’est-à-dire que chacun de ces Layers sera une classe. Pour chacune des deux classes, il faudra implémenter les méthodes
- feedforward : pour calculer le résultat de l’opération.
- backpropagation : pour calculer le gradient.
- update : pour mettre-à-jour les paramètres.
La méthode feedforward prendra en entrée un vecteur ![]() et renverra le résultat du calcul
et renverra le résultat du calcul ![]() . Ensuite ce résultat devra être stockée afin de pouvoir être utilisé par backpropagation.
. Ensuite ce résultat devra être stockée afin de pouvoir être utilisé par backpropagation.
La méthode backpropagation est plus subtile. Comme expliqué dans l’article sur la Backpropgation, pour propager le gradient on a besoin de deux choses :
- Le gradient du score par rapport à la sortie de l’opération.
- Et la valeur d’entrée de l’opération.
Ainsi la méthode backpropagation prendra en entrée ![]() , l’entrée feedforward, et le gradient du score par rapport à
, l’entrée feedforward, et le gradient du score par rapport à ![]() et renverra le gradient du score par rapport à
et renverra le gradient du score par rapport à ![]() .
.
Dans le cas de la transformation linéaire, en plus de calculer le gradient par rapport à ![]() et il devra aussi calculer le gradient par rapport à ses paramètres
et il devra aussi calculer le gradient par rapport à ses paramètres ![]() et
et ![]() .
.
La méthode update prendra en paramètre le learning-rate et devra mettre à jour le poids l’aide du learning-rate et du gradient calculé par la méthode backpropagation.
C’est parti pour coder un réseau de neurones
Les vecteurs, les matrices et les opérations seront faites à partir de la librairie numpy, qui peut être installée avec PIP par la commande :
1 | pip install numpy |
La classe Linear
La première opération va être implémentée par la classe Linear (son équivalent en PyTorch est torch.nn.Linear, et son équivalent sous Keras/Tensorflow est keras.layers.Dense).
Voici son implémentation :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | class Linear: def __init__(self, input_dimension, output_dimension): self.input_dimension = input_dimension # input dimension self.output_dimension = output_dimension # output dimension self.weight = numpy.random.normal(loc=0.0, scale=1.0, size=(input_dimension, output_dimension)) # Weight self.bias = numpy.zeros(shape=(output_dimension,)) # Bias self.gradient_weight = numpy.zeros(shape=(self.input_dimension, self.output_dimension)) # Weight gradient self.gradient_bias = numpy.zeros(shape=(self.output_dimension,)) # Bias gradient def feedforward(self, X): Y = numpy.matmul(X, self.weight) + self.bias # Linear transformation return Y def backpropagation(self, X, gradient_Y): self.gradient_bias += gradient_Y # gradient bias self.gradient_weight += numpy.tensordot(X, gradient_Y, axes=0) # gradient weight gradient_X = numpy.matmul(self.weight, gradient_Y) # gradient X return gradient_X def update(self, learning_rate): self.weight -= learning_rate * self.gradient_weight # Update weight self.bias -= learning_rate * self.gradient_bias # Update bias self.gradient_weight = numpy.zeros(shape=(self.input_dimension, self.output_dimension)) # reset gradient self.gradient_bias = numpy.zeros(shape=(self.output_dimension,)) # reset gradient |
Examinons pas à pas ce code. La construction est définie par la méthode __init__. Elle prend en paramètre la dimension de l’entrée et la dimension de sortie. Dans __init__ on initialise les attributs suivants :
- self.input_dimension : la dimension de l’entrée.
- self.output_dimension : La dimension de sortie.
- self.weight : le poids initialisé aléatoirement.
- self.bias : le biais.
- self.gradient_weight : la somme des gradients par rapport au poids.
- self.gradient_bias : la somme des gradients par rapport au biais.
La méthode feedforward ne présente pas de difficulté. Elle consiste à effectuer l’opération. A noter que le format de X doit être ![]() , où
, où ![]() vaut input_dimension, et donc il faut prendre la convention d’écriture
vaut input_dimension, et donc il faut prendre la convention d’écriture ![]() , avec la matrice
, avec la matrice ![]() à gauche.
à gauche.
La méthode backpropagation prend en entrée ![]() , la même valeur d’entrée que feedforward, et le gradient du score par rapport à la sortie. A partir de ces valeurs, elle calcule le gradient par rapport au biais et au poids, puis l’ajoute à self.bias et self.weight. Et ensuite elle renvoie la valeur du gradient par rapport à l’entrée.
, la même valeur d’entrée que feedforward, et le gradient du score par rapport à la sortie. A partir de ces valeurs, elle calcule le gradient par rapport au biais et au poids, puis l’ajoute à self.bias et self.weight. Et ensuite elle renvoie la valeur du gradient par rapport à l’entrée.
La raison pour laquelle le gradient par rapport au poids est donnée par la ligne de code numpy.tensordot(X, gradient_Y, axes=0), vient du fait que si ![]() , et que si
, et que si ![]() est la fonction de score, alors
est la fonction de score, alors
![]()
où ![]() est la matrice des dérivées partielle par rapport au coefficients de la matrice
est la matrice des dérivées partielle par rapport au coefficients de la matrice ![]() ,
, ![]() est le gradient par rapport à
est le gradient par rapport à ![]() et
et ![]() est produit tensoriel du vecteur
est produit tensoriel du vecteur ![]() avec le vecteur
avec le vecteur ![]() (le résultat est alors une matrice).
(le résultat est alors une matrice).
La méthode update se contente de mettre à jour self.bias et self.weight à partir du learning_rate et reinitialise les valeurs self.gradient_weight et self.gradient_bias à 0.
La classe Sigmoid
La classe Sigmoid représente l’opération d’activation avec la fonction sigmoïde. Son implémentation est plus simple car cette opération n’a pas de paramètres tels que le poids ou le biais. Si tu as bien suivi l’implémentation de Linear, alors tu devrais être capables d’implémenter Sigmoid toi-même.&bnsp;👌
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | class Sigmoid: def __init__(self): pass def feedforward(self, X): Y = 1 / (1 + numpy.exp(-X)) # sigmoid activation return Y def backpropagation(self, X, gradient_Y): expo = numpy.exp(-X) gradient_X = gradient_Y * expo/numpy.square(1+expo) # gradient X return gradient_X def update(self, learning_rate): pass # Nothing to do |
Même si ce code est très simple, regardons le pas-à-pas. La construction __init__ ne nécessite pas de paramètres.
La méthode feedforward applique la fonction ![]() sur chaque composante du vecteur
sur chaque composante du vecteur ![]() .
.
Ensuite, la méthode backpropagation multiplie le gradient par rapport à ![]() par la dérivée de sigmoid
par la dérivée de sigmoid ![]() , afin d’obtenir le gradient par rapport à
, afin d’obtenir le gradient par rapport à ![]() .
.
Enfin, la méthode update ne fait rien, car il n’y a pas de paramètres.
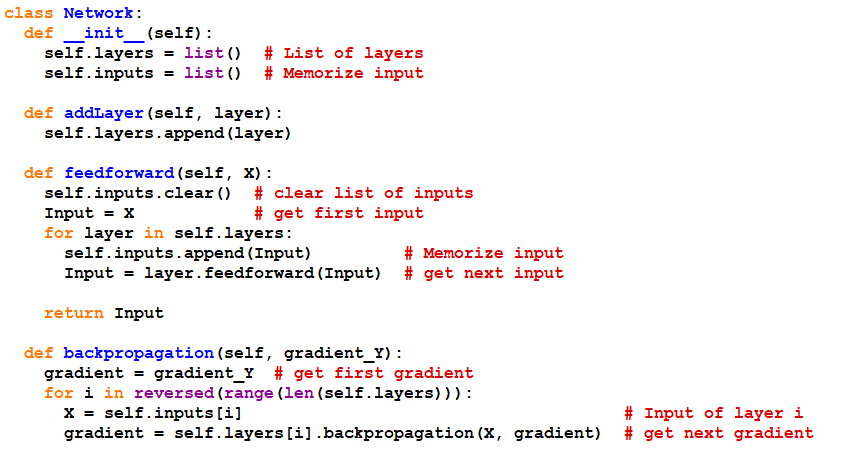
La classe Network
La classe Network représentera le modèle Multi-Layer-Perceptron. Il se chargera de contenir l’architecture du réseau, à savoir la liste des Layers.
Afin d’imiter l’interface de keras/Tensorflow, pour construire le réseaux on créera une méthode addLayer en passant en paramètre l’une des classes Linear ou Sigmoid que l’on vient de construire.
Une méthode fit permettra d’entraîner le réseau. Il prendra en paramètres :
- Une matrice représentant le data set d’entraînement, de (format nombre d’échantillons, nombre de features).
- Une matrice des valeurs cibles, de (format nombre d’échantillons, nombre de composantes de la valeur cible).
- Le learning-rate.
- Le nombre d’époques, c’est à dire le nombre fois que l’apprentissage doit parcourir le data set d’entraînement tout entier.
Voici son implémentation :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 | class Network: def __init__(self): self.layers = list() # List of layers self.inputs = list() # Memorize input def addLayer(self, layer): self.layers.append(layer) def feedforward(self, X): self.inputs.clear() # clear list of inputs Input = X # get first input for layer in self.layers: self.inputs.append(Input) # Memorize input Input = layer.feedforward(Input) # get next input return Input def backpropagation(self, gradient_Y): gradient = gradient_Y # get first gradient for i in reversed(range(len(self.layers))): X = self.inputs[i] # Input of layer i gradient = self.layers[i].backpropagation(X, gradient) # get next gradient def update(self, learning_rate): for layer in self.layers: layer.update(learning_rate) # Update all layers def fit(self, xData, yData, epochs, learning_rate): for epoch in range(epochs): # Compute MSE score pred = self.feedforward(xData) mse = sklearn.metrics.mean_squared_error(yData, pred) print("epoch =", epoch, "score =", mse) for i in range(len(xData)): X = xData[i] # Input value Y = self.feedforward(X) # Output value target = yData[i] # target value score_gradient = Y-target # gradient of the score self.backpropagation(score_gradient) # Compute gradients self.update(learning_rate) # udpate weights |
Encore une fois examinons ce code. Le constructeur __init__ ne nécessite pas de paramètres car la construction du réseau passe par la méthode addLayer. L’attribut self.layers contiendra la liste des Layers et self.inputs servira à mémoriser les calculs de feedforward afin de les utiliser lors de backpropagation.
La méthode addLayer prend en paramètre l’une des couches Linear ou Sigmoid et l’ajoutera dans l’attribut self.layers.
La méthode feedforward calcule le résultat de chaque Layer et renvoie le résultat du dernier calcul. De plus en interne, il stocke les résultats intermédiaires dans la liste self.inputs afin d’être utilisés par Backpropagation.
Ensuite, la méthode backpropagation calcule le gradient sur chaque Layer en sens inverse.
Quant à la méthode update, elle met à jour de chaque Layer.
La méthode fit est la boucle d’entraînement. Au début de chaque époque, on affiche le score et ensuite on parcourt le data set pour appliquer la méthode du gradient. A noter que feedforward est censé prendre en paramètre un vecteur, mais il se trouve qu’avec notre implémentation il peut prendre un data set (mais attention, ce n’est pas vrai pour la méthode backpropagation, le paramètre ne peut pas être un data set de gradients, à cause de la manière dont ont fait les multiplications).
Testons note modèle
Maintenant que tout est prêt, pour vérifier que tout se passe bien, je te propose de tester avec le code suivant :
1 2 3 4 5 6 7 8 9 10 | xData = numpy.array([[0,0], [1,0], [0,1], [1,1]]) yData = numpy.array([0, 1, 1, 0]) model = Network() model.addLayer( Linear(2, 5) ) model.addLayer( Sigmoid() ) model.addLayer( Linear(5, 1 )) model.addLayer( Sigmoid() ) model.fit(xData, yData, epochs=100, learning_rate=10) |
Le data set est simplement le XOR et la structure du modèle est constituée de la manière suivante.
- Une première couche Linéaire transformant un vecteur d’entrée de taille 2 en un vecteur de taille 5.
- Cette couche est activée par Sigmoid.
- Ensuite, une couche Linéaire transformant un vecteur de taille 5 en un vecteur de taille 1.
- Et cette dernière est activée Sigmoid.
Autrement dit c’est un modèle avec une seule couche cachée de 5 neurones 👍.
Et voici ce qu’affiche l’apprentissage :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 | epoch = 0 score = 0.3245590739686766 epoch = 1 score = 0.4146711879125931 epoch = 2 score = 0.3869972020093815 epoch = 3 score = 0.38678212862030814 epoch = 4 score = 0.37886474212822074 epoch = 5 score = 0.38918271322015174 epoch = 6 score = 0.39453135272100553 epoch = 7 score = 0.34532390585725425 epoch = 8 score = 0.2873546196606331 epoch = 9 score = 0.28103016135035214 epoch = 10 score = 0.24838004595286692 epoch = 11 score = 0.2442120052977134 epoch = 12 score = 0.24126414110226635 epoch = 13 score = 0.2379957471969403 epoch = 14 score = 0.2341438999358595 epoch = 15 score = 0.22959892096553855 epoch = 16 score = 0.22439844398421283 epoch = 17 score = 0.21874479329043392 epoch = 18 score = 0.21295148919463694 epoch = 19 score = 0.20732761803567168 epoch = 20 score = 0.20208115535632037 epoch = 21 score = 0.19729927665304936 epoch = 22 score = 0.1929856256386121 epoch = 23 score = 0.18910675919333242 epoch = 24 score = 0.18562418145979548 epoch = 25 score = 0.18251050067283278 epoch = 26 score = 0.1797534260048746 epoch = 27 score = 0.17734998596823853 epoch = 28 score = 0.17529301597919245 epoch = 29 score = 0.17355516046178215 epoch = 30 score = 0.17208057926934006 epoch = 31 score = 0.17079351526158423 epoch = 32 score = 0.16962030874086026 epoch = 33 score = 0.16850872778696102 epoch = 34 score = 0.16743259975818736 epoch = 35 score = 0.16638452714191262 epoch = 36 score = 0.16536612975424314 epoch = 37 score = 0.16438139368508528 epoch = 38 score = 0.16343361803939443 epoch = 39 score = 0.16252455973882574 epoch = 40 score = 0.16165453284927198 epoch = 41 score = 0.16082278605618622 epoch = 42 score = 0.16002787801269958 epoch = 43 score = 0.15926796666152523 epoch = 44 score = 0.15854100738765103 epoch = 45 score = 0.15784487888234278 epoch = 46 score = 0.15717745812556508 epoch = 47 score = 0.15653666175818962 epoch = 48 score = 0.15592046606543944 epoch = 49 score = 0.15532691363231338 epoch = 50 score = 0.154754111747969 epoch = 51 score = 0.1542002256359973 epoch = 52 score = 0.1536634682920445 epoch = 53 score = 0.15314208788082262 epoch = 54 score = 0.1526343531071915 epoch = 55 score = 0.15213853661234666 epoch = 56 score = 0.1516528961776719 epoch = 57 score = 0.1511756532927297 epoch = 58 score = 0.15070496842248168 epoch = 59 score = 0.15023891206180395 epoch = 60 score = 0.14977543036398155 epoch = 61 score = 0.149312303742063 epoch = 62 score = 0.14884709632766338 epoch = 63 score = 0.14837709347704198 epoch = 64 score = 0.14789922356386923 epoch = 65 score = 0.14740995898480017 epoch = 66 score = 0.14690518947329517 epoch = 67 score = 0.14638005824451572 epoch = 68 score = 0.1458287478519693 epoch = 69 score = 0.14524419744642092 epoch = 70 score = 0.14461772569341466 epoch = 71 score = 0.14393852292700945 epoch = 72 score = 0.1431929607920166 epoch = 73 score = 0.1423636457925085 epoch = 74 score = 0.14142811262459323 epoch = 75 score = 0.14035701212440393 epoch = 76 score = 0.13911159810150414 epoch = 77 score = 0.13764026778371075 epoch = 78 score = 0.13587389951040185 epoch = 79 score = 0.13371986486313048 epoch = 80 score = 0.13105513845995911 epoch = 81 score = 0.12772049694849535 epoch = 82 score = 0.12352159671313172 epoch = 83 score = 0.11825055787756829 epoch = 84 score = 0.1117542980760137 epoch = 85 score = 0.10408572123111082 epoch = 86 score = 0.09574809823036308 epoch = 87 score = 0.08791400451329688 epoch = 88 score = 0.08226888578814068 epoch = 89 score = 0.08020607223929425 epoch = 90 score = 0.08205591160846737 epoch = 91 score = 0.08670716448125033 epoch = 92 score = 0.0872903929422535 epoch = 93 score = 0.06589148216594312 epoch = 94 score = 0.03259843272426774 epoch = 95 score = 0.018032060780678788 epoch = 96 score = 0.0101096739415762 epoch = 97 score = 0.008707276950179397 epoch = 98 score = 0.007992233586528036 epoch = 99 score = 0.007436081265603082 |
Une fois le code exécutée tu devrais pour voir que le score diminue vers 0, ce qui signifie que le réseau a bien appris sur le data set. 😀
Pour terminer voici le code complet de tout ce qu’on a fait :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 | import numpy import pandas import sklearn import sklearn.metrics class Linear: def __init__(self, input_dimension, output_dimension): self.input_dimension = input_dimension # input dimension self.output_dimension = output_dimension # output dimension self.weight = numpy.random.normal(loc=0.0, scale=1.0, size=(input_dimension, output_dimension)) # Weight self.bias = numpy.zeros(shape=(output_dimension,)) # Bias self.gradient_weight = numpy.zeros(shape=(self.input_dimension, self.output_dimension)) # Weight gradient self.gradient_bias = numpy.zeros(shape=(self.output_dimension,)) # Bias gradient def feedforward(self, X): Y = numpy.matmul(X, self.weight) + self.bias # Linear transformation return Y def backpropagation(self, X, gradient_Y): self.gradient_bias += gradient_Y # gradient bias self.gradient_weight += numpy.tensordot(X, gradient_Y, axes=0) # gradient weight gradient_X = numpy.matmul(self.weight, gradient_Y) # gradient X return gradient_X def update(self, learning_rate): self.weight -= learning_rate * self.gradient_weight # Update weight self.bias -= learning_rate * self.gradient_bias # Update bias self.gradient_weight = numpy.zeros(shape=(self.input_dimension, self.output_dimension)) # reset gradient self.gradient_bias = numpy.zeros(shape=(self.output_dimension,)) # reset gradient class Sigmoid: def __init__(self): pass def feedforward(self, X): Y = 1 / (1 + numpy.exp(-X)) # sigmoid activation return Y def backpropagation(self, X, gradient_Y): expo = numpy.exp(-X) gradient_X = gradient_Y * expo/numpy.square(1+expo) # gradient X return gradient_X def update(self, learning_rate): pass # Nothing to do class Average: def __init__(self): pass def feedforward(self, X): Y = X / numpy.sum(X, axis=-1) return Y def backpropagation(self, X, gradient_Y): expo = numpy.exp(-X) gradient_X = gradient_Y * expo/numpy.square(1+expo) # gradient X return gradient_X def update(self, learning_rate): pass # Nothing to do class Network: def __init__(self): self.layers = list() # List of layers self.inputs = list() # Memorize input def addLayer(self, layer): self.layers.append(layer) def feedforward(self, X): self.inputs.clear() # clear list of inputs Input = X # get first input for layer in self.layers: self.inputs.append(Input) # Memorize input Input = layer.feedforward(Input) # get next input return Input def backpropagation(self, gradient_Y): gradient = gradient_Y # get first gradient for i in reversed(range(len(self.layers))): X = self.inputs[i] # Input of layer i gradient = self.layers[i].backpropagation(X, gradient) # get next gradient def update(self, learning_rate): for layer in self.layers: layer.update(learning_rate) # Update all layers def fit(self, xData, yData, epochs, learning_rate): for epoch in range(epochs): # Compute MSE score pred = self.feedforward(xData) mse = sklearn.metrics.mean_squared_error(yData, pred) print("epoch =", epoch, "score =", mse) for i in range(len(xData)): X = xData[i] # Input value Y = self.feedforward(X) # Output value target = yData[i] # target value score_gradient = Y-target # gradient of MSE self.backpropagation(score_gradient) # Compute gradients self.update(learning_rate) # udpate weights xData = numpy.array([[0,0], [1,0], [0,1], [1,1]]) yData = numpy.array([0, 1, 1, 0]) model = Network() model.addLayer( Linear(2, 5) ) model.addLayer( Sigmoid() ) model.addLayer( Linear(5, 1 )) model.addLayer( Sigmoid() ) model.fit(xData, yData, epochs=100, learning_rate=10) |
Exercice
Si jusqu’ici tout se passe bien, tu peux tester sur le data set MNIST des chiffres écrit à la main. Tu peux le télécharger grâce à la commande suivante :
1 2 3 | from keras.datasets import mnist (train_X, train_y), (test_X, test_y) = mnist.load_data() |
Afin d’en apprendre plus sur ce data set, tu peux regarder ici. Le MLP permet facilement d’avoir des résultats satisfaisants (au moins 80% de bonnes prédictions), même s’il y a d’autres architectures qui font mieux comme les réseaux de convolutifs.
⚠ Attention à ne pas oublier de normaliser le data set en divisant par 255, parce qu’un réseau de neurones n’est pas fait pour manger 🍕 des valeurs trop grandes. 👍
Pour aller plus loin
Maintenant que tu sais coder un réseau de neurones,n ‘hésite pas à dire en commentaire ce que tu as pensé de ce tutoriel. 👌
Si tu veux t’entraîner à coder 🤔, tu peux aller plus loin en implémentant les fonctionnalités suivantes :
- D’autres fonctions d’activation comme : tanh, ReLu, softmax,…
(Attention softmax est plus compliqué que ça en a l’air car l’exponentiel peut produire des valeurs infinies…😬) - La méthode de gradient par batch et mini-batch.
- D’autre méthodes de descente de gradient que tu peux trouver ici.




0 commentaire